Suppose that two cells within at least one large container (box, column, row) have exactly the
same two candidates left as the only possibilities for these two cells. Then, one can exclude
those two candidates from all the rest of the cells within that large container(s).
Consider:
- A cell outside of those two cells
- That cell is also within the paired cells' common large container(s)
- Let that cell solve as one of two paired candidates
- Then both of the original cells would be forced to equal the other candidate.
Since no candidate can appear twice within the same large container, this is forbidden.
One may notice that most proofs of ideas are proofs by contradication. This will be the case
with most techniques. To eliminate a candidate in the possibility matrix, one generally
must show that cell X = candidate N violates the rules.
The following is an example of Naked Pairs .
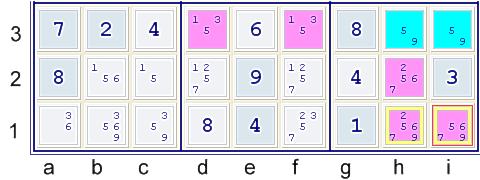
In this example,note that cells h3,i3 both have only 5,9 left as possibilities.
Since cells h3,i3 are both contained within row 3 and box h2, we can exclude 5's from d3,f3,h1,h2,i1.
We can also exclude 9's from h1,i1. In a proof, this could be presented as follows:
- Pair 59 at hi3 forbids df3,h2,hi1=5 and hi1=9.
Although the above presentation of proof lingo is my preferred style, one might also see
other ways to present the same idea such as:
- hi3=Naked Pair 59=>df3,h12,i1~5;hi1~9.
- NP 59 = hi3 => df3,h2,i12<>5;hi1<>9
- hi3={59} forbids df3,h2,i12=5 and forbids hi1=9.
The choice of proof presentation is not standard, so one must try to logically decipher each proof
writer's codes.
The same idea can be extended to any number of cells contained within a common container.
Thus, if for example we had:(the grid above does not illustrate the following example.)
- a1 = 123
- a2 = 123
- a3 = 123
One could safely conclude:
- Forbids b123,c123,a456789=123
One idea that bears mentioning here is that it is not necessary that all the possibilities be
fully represented, for example:
- a1 = 12
- a2 = 23
- a3 = 13
- Forbids b123,c123,a456789=123
Hopefully the reasoning for this is clear. In either case, one could present this idea in a proof as:
- Triplet 123 at a123 forbids bc123,a456789=123.
.
The proof of extending this idea beyond two cells can be done many ways. The easiest way, in my
opinion is to just think of it inductively: No matter what a1 equals, in the first example, there
will be a naked pair in a23.
Next, we extend this technique using Hidden Pairs, Triples and Quads